2019.12.05(pm): Softmax function

Machine learning problems can be divided into classification and regression. Classification is a matter of which class the data belongs to, and regression is a problem of predicting consecutive numbers in the input data. As such, the output value of the neural network can be obtained using the identity function and the softmax function. This plays an important role in classification and regression.

In addition, problem solving in machine learning takes place in two stages: learning and inference. The model is trained in the learning phase, and the inference (classification) is performed on the unknown data with the previously trained model in the inference phase. In the inference step, it is common to omit the softmax function of the output layer. The reasoning process is also called forward propagation of neural networks. On the other hand, when training neural networks, we use softmax functions in the output layer.

Softamax function

Softmax is a kind of activation function. Softmax normalizes all the input values ​​to the value between 0 and 1, and the sum of the output values ​​is always a function.

Initially, you should configure the output as many as the number of classes you want to classify. The class given the largest output value is considered to have the highest probability. However, the Softmax result is [0.4, 0.3, 0.2, 0.1] and the first 0.4 and [0.7, 0.1, 0.1, 0.1] and the first 0.7 will be different.

The formula for obtaining Softmax is as follows.

If you look closely, you can see that the order of the input values ​​is the same as the order of the output values. After all, the largest value was already the largest value before Softmax.

Therefore, it is omitted in order to speed up the computation in the reasoning (operation) stage. If you connect the softmax result to the input of one hot encoder, only the largest value is true and the rest is false.

Let’s run the code below

import numpy as np
import matplotlib.pyplot as plt
 
def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum()
 
x = np.array([2.0,2.0,2.0,4.0])
 
y = softmax(x)
 
print(np.sum(y))
 
ratio = y
labels = y
 
plt.pie(ratio, labels=labels, shadow=True, startangle=90)
plt.show()

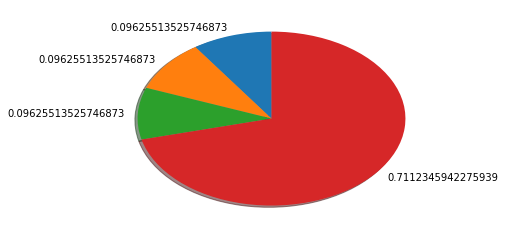
You can get a graph like this

Softmax input values: 2.0, 2.0, 2.0, 4.0

Softmax output values: 0.1, 0.1, 0.1, 0.7 (Approximate value.)

The reason why the output does not fit correctly is because of exp (x). Softmax uses the values ​​e ^ 1 = 2.718 and e ^ 2 = 7.389 instead of 1 and 2. In other words, as the input value increases, the slope increases and a larger difference occurs.