2019.11.02(pm): Bayes’s Theorem and MLE vs MAP

Bayes’s Theorem

Called Bayes’s theorem or Bayes’s rule or Bayes’ law, this is a conditional probability equation (X2: model, X1: observation)

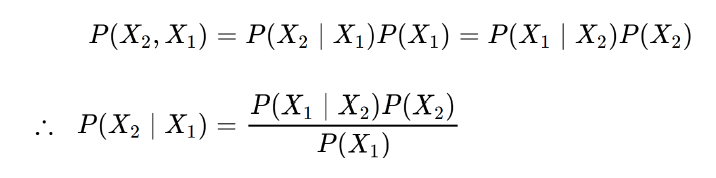
Bayesian probabilities are probability transforms that allow the posterior probability to be calculated using prior and likelihoods. Bayesian probabilities mostly occur when classification and detection problems occur in image processing. In other words, Bayesian probabilities are generally the first thing people think about when they need something mathematical in their methodology.

Likelihood: p (S | X), the probability that the data (observed value) comes from a model

Prior probability: p (X), the a priori probability that the observer has for the system or model before the observation is made. For example, p (male), p (female), etc. representing the composition ratio of male and female correspond to prior probability.

Posterior probability: p (X | S), the probability that the event occurred in a particular model after the event occurred (after observation has progressed)

There are two ways to solve the classification problem using probability.

The MLE (Maximum Likelihood) method and the MAP (Maximum A Posteriori) method.

Let S be the observation, and X is the class (or model) from which it came. For example, consider the problem of judging the back of a person sitting in a restaurant (S) and determining whether the person’s gender is male or female (X).

MLE (Maximum Likelihood)

The MLE method compares the probability p (S | male) of such a back appearance in a man and the probability p (S | female) of such a back in a woman and selects the class with the highest probability, that is, the likelihood. Way.

MAP (Maximum A Posteriori)

In the MAP method, a back pattern called S was found, and it is the method of selecting the class (gender) which has the greater value of the two, comparing the probability p (male | S) to that of male and the probability p (female | S) to that of female. . In other words, Bayes’ theorem is used to calculate posterior probability in MAP as a method of maximizing posterior prabability.

However, the difference between MLE and MAP becomes clear when considering gender ratios of men and women. If 70% of the population is male and 30% are female. MLE completely ignores the gender ratio of men and women and compares only the probability of having the back in men and the probability of having the back in women. On the other hand, MAP is a method of determining the final class considering not only the probability of the back of each gender but also the gender ratio of men and women.

Using the Bayes’ theorem, the probability of a man behind MAP is as follows.

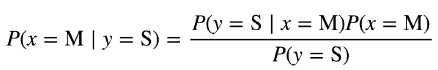
In summary, MAP method is more accurate classification method than MLE. In many cases, however, most people do not know the prior probability, p (male), p (female), so they often solve the problem simply by setting p (male) = p (female). Becomes the same as MLE.

Bayesian Probability Example Using pgmpy