2019.12.01(pm): Stochastic Gradient Decent method

Let’s talk about the cost function again. The cost function for learning the weights of the Adaline (Adaptive Linear Neuron) is defined in relation to the i th observation in the training data set as follows:

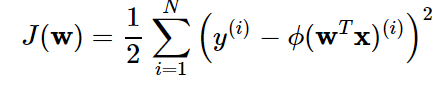
where the ϕ is an activation function.

To find the weights that minimize our cost function, we can use optimization algorithm called gradient descent:

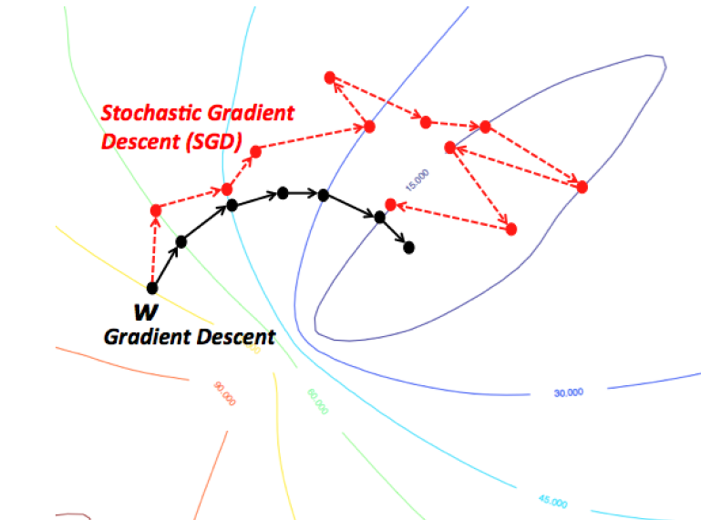
Gradient descent was a method of finding the optimal value (slope) to reduce the magnitude of the loss function (cost). The biggest problem with gradient descent, however, is that it reads a huge amount of learning data at once and then moves on to the next step. Doing so will cause the batch size to become so large that the computational speed will be too slow.

So introduced was SGD, a method of setting batch size to 1.

To minimize cost functions, gradients from batch gradient descents are calculated over the entire training set

If you have a huge dataset with millions of data points, running a batch minimum gradient descent can be costly because you need to reevaluate the entire training dataset every step with the global minimum.

Therefore, the probability gradient descent method uses (Δw), defined above, to use the following update instead of updating the weight based on the sum of the cumulative errors for all samples x (i).

reference: https://www.bogotobogo.com/python/scikit-learn/scikit-learn_batch-gradient-descent-versus-stochastic-gradient-descent.php

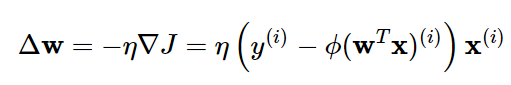
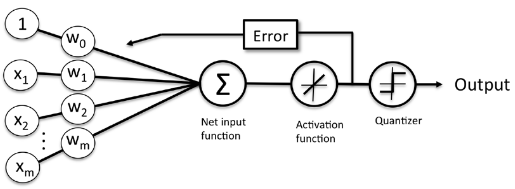
Advantages of Stochastic Gradient Descent

1. It is easier to fit into memory due to a single training sample being processed by the network
2. It is computationally fast as only one sample is processed at a time
3. For larger datasets it can converge faster as it causes updates to the parameters more frequently
4. Due to frequent updates the steps taken towards the minima of the loss function have oscillations which can help getting out of local minimums of the loss function (in case the computed position turns out to be the local minimum)

Disadvantages of Stochastic Gradient Descent

1. Due to frequent updates the steps taken towards the minima are very noisy. This can often lead the gradient descent into other directions.
2. Also, due to noisy steps it may take longer to achieve convergence to the minima of the loss function
3. Frequent updates are computationally expensive due to using all resources for processing one training sample at a time
4. It loses the advantage of vectorized operations as it deals with only a single example at a time

Advantage vs Disadvantages of Stochatic Gradient Descent : https://medium.com/@divakar_239/stochastic-vs-batch-gradient-descent-8820568eada1