Feature Engineering
Feature engineering is the process of using domain knowledge of the data to create features that make machine learning algorithms work. Feature engineering is fundamental to the application of machine learning, and is both difficult and expensive. The need for manual feature engineering can be obviated by automated feature learning(from : https://en.wikipedia.org/wiki/Feature_engineering )
For example, suppose you are watching a soccer game and you are predicting the outcome of the game. Can you predict a win or loss just by the start of the match? Or can you predict which team will win by the age of the football manager? Probably difficult. However, if you look at the number of goals scored by each team player, and the result of winning or losing, you will be able to predict more accurately.
As mentioned above, machine learning performance is highly dependent on the amount and quality of the data. So it’s very important to choose which features to choose.
Dimension Reduction
Dimensional reduction is also called feature extraction. If we have three independent variables describing one dependent variable, we do not need all three features. This is because some features may be represented by a combination of other features and some features may be completely incompatible with certain features.
In other words, the latent space that can explain the observations well can be smaller than the actual observation space, and the identification of the latent space based on the samples above the observation space is called the dimensionality reduction technique. There are two ways to reduce the dimension of the data: feature selection and feature extraction.
Feature Selection
The purpose of feature selection is to select a subset of all features to create a concise feature set. In the previous football situation, if we think that the manager’s age does not affect the outcome prediction, we can remove that feature from the full feature set. This feature selection removes unnecessary features (variables) from the original data.
This feature selection can be done by the analyst using a prior background, but can also use automatic feature selection methods. These methods remove some of the features and check their performance if they improve, which is the default behavior of most feature selection algorithms.
Feature Extraction
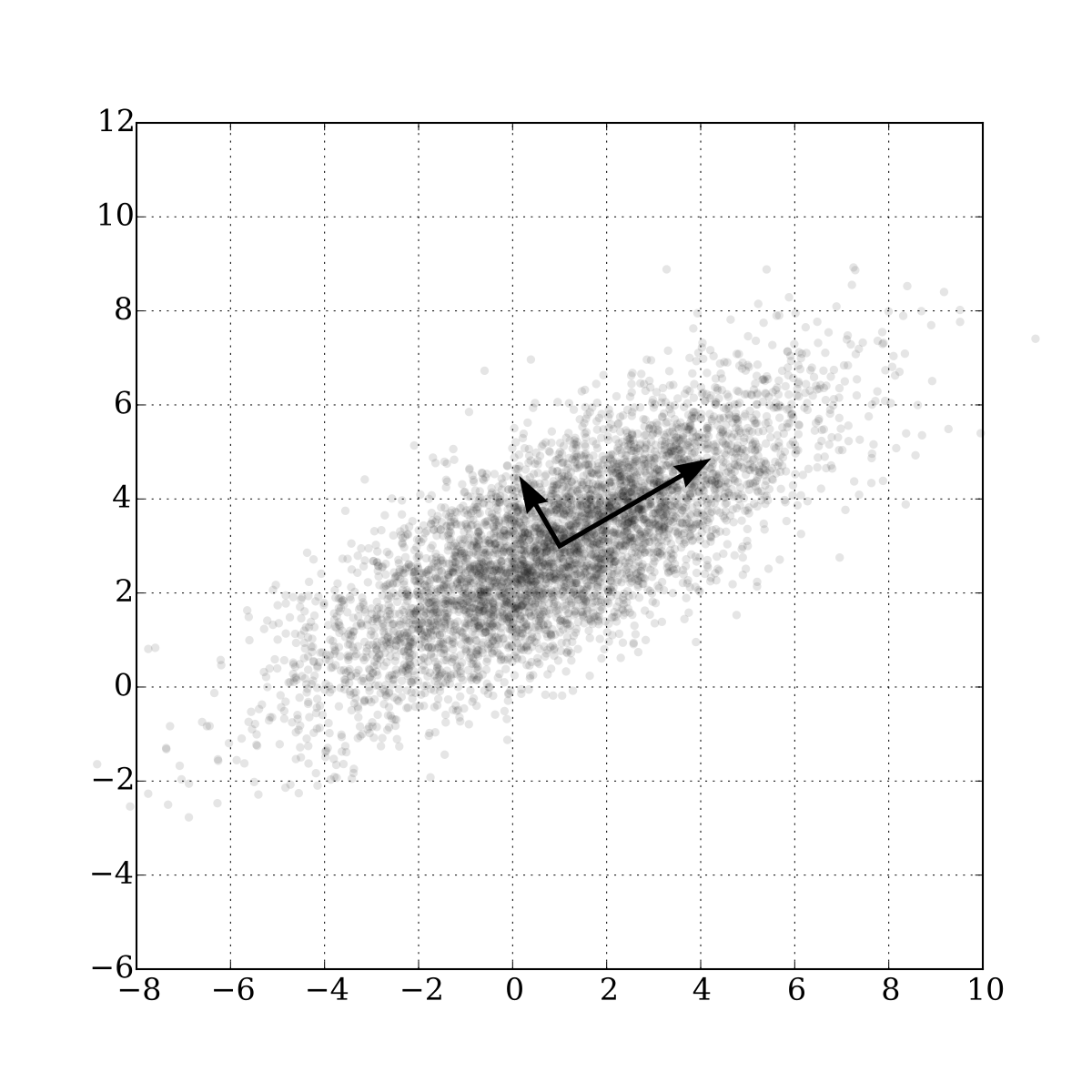
Feature extraction attempts to create a new feature with a combination of original features. For example, Principal Compnent Analysis is the most basic and popular dimension reduction technique. The principle of operation is to find an orthogonal major axis from the data and project all data onto that axis. In this case, the projection function that makes the original data projected data is equivalent to creating a new feature that consists of a linear combination of the original features.
Dimension reduction practical code using feature selection
Select numerical properties based on variance
# import library from sklearn import datasets from sklearn.feature_selection import VarianceThreshold # loading data iris = datasets.load_iris() # feature and target features = iris.data target = iris.target # making threshold thresholder = VarianceThreshold(threshold=.5) # select feature has high variance than threshold features_high_variance = thresholder.fit_transform(features) # confirm feature_high variance features_high_variance[0:3]

# confirm variance thresholder.variances_
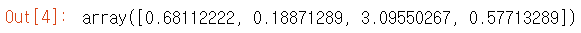
# import library from sklearn.preprocessing import StandardScaler # standarzation of feature array scaler = StandardScaler() features_std = scaler.fit_transform(features) # calculate variance selector = VarianceThreshold() selector.fit(features_std).variances_
Select binary properties based on variance
# import library
from sklearn.feature_selection import VarianceThreshold
# making feature array
# feature 0: 80%가 class 0
# feature 1: 80%가 class 1
# feature 2: 60%가 class 0, 40%는 class 1
features = [[0, 1, 0],
[0, 1, 1],
[0, 1, 0],
[0, 1, 1],
[1, 0, 0]]
# selection depending on variance
thresholder = VarianceThreshold(threshold=(.75 * (1 - .75)))
thresholder.fit_transform(features)

Dealing with Correlated Characteristics
# import library
import pandas as pd
import numpy as np
# making feature array with correlated characteristics
features = np.array([[1, 1, 1],
[2, 2, 0],
[3, 3, 1],
[4, 4, 0],
[5, 5, 1],
[6, 6, 0],
[7, 7, 1],
[8, 7, 0],
[9, 7, 1]])
# Convert array to DataFrame
dataframe = pd.DataFrame(features)
# making correlation matrix
corr_matrix = dataframe.corr().abs()
# Select upper triangle of corr_matrix
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(np.bool))
# Find Index of column bigger than 0.95, corr_coefficient
to_drop = [column for column in upper.columns if any(upper[column] > 0.95)]
# Remove feature
dataframe.drop(dataframe.columns[to_drop], axis=1)

dataframe.corr()
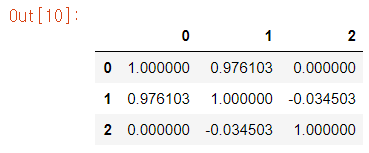
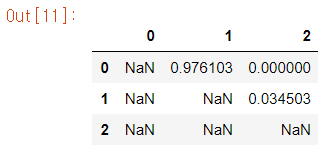
upper
Deleting features not related to Classification
# import library
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2, f_classif
# load data
iris = load_iris()
features = iris.data
target = iris.target
# convert type as integer
features = features.astype(int)
# Select the two values with the largest chi-square
chi2_selector = SelectKBest(chi2, k=2)
features_kbest = chi2_selector.fit_transform(features, target)
# Result
print("원본 특성 개수:", features.shape[1])
print("줄어든 특성 개수:", features_kbest.shape[1])

# Select the two attributes with the highest F-values
fvalue_selector = SelectKBest(f_classif, k=2)
features_kbest = fvalue_selector.fit_transform(features, target)
# Result
print("원본 특성 개수:", features.shape[1])
print("줄어든 특성 개수:", features_kbest.shape[1])

# import library
from sklearn.feature_selection import SelectPercentile
# Select the top 75% attribute of the largest F-value.
fvalue_selector = SelectPercentile(f_classif, percentile=75)
features_kbest = fvalue_selector.fit_transform(features, target)
# Result
print("원본 특성 개수:", features.shape[1])
print("줄어든 특성 개수:", features_kbest.shape[1])