2020.03.08(am): K-means Clustering

Unsupervised learning

There are two types of machine learning algorithms: supervised learning and unsupervised learning. Unsupervised learning refers to all kinds of machine learning that must teach a learning algorithm without any known output or information.

The most difficult thing in unsupervised learning is to evaluate whether the algorithm has learned something useful. Unsupervised learning usually uses unlabeled data so you don’t know what is the correct output. So it’s hard to determine which model is doing well. It is impossible to ask a computer directly what a person wants. And in order to evaluate the results of unsupervised learning, it is often a good idea to identify them in person. Therefore, unsupervised learning algorithms are often used in the data exploration stage.

Clustering

One of the unsupervised learning is clustering. Clustering algorithms group data together similarly. For example, if you want to distinguish mail from your inbox into spam, business mail, or other mail, you can consider grouping messages with similar characteristics without specifying any labels. As another example, iPhone users can see in their photo albums that distinguish the faces of people who have taken their own photos (I don’t know if it’s possible in Galaxy). This is also an example of clustering that extracts and distinguishes similar features.

K-means Clustering

k-means clustering is the simplest and most widely used clustering algorithm. This algorithm finds the cluster center that represents a certain area of ​​data. The algorithm repeats two steps. The first assigns points of data to the nearest cluster center. The second specifies the cluster center again with the average of the data points assigned to the cluster. The algorithm terminates when there are no changes in the data points assigned to the cluster.

Argorithm

Given a set of n d-dimensional data objects (x1, x2, …, xn), the k-average algorithm selects n data objects with k set S = {S1, S2,… , Sk}. In other words, when μi is the center point of the set Si.

Cluster configuration: The Euclidean distance from each data to μi of each cluster is calculated to find the nearest cluster from the data and allocate the data.

Cluster-centered readjustment: resets μi to the center of gravity of the data in each cluster.

The following is the k-means clustering algorithm applied to the example data set.

from mglearn import *
plots.plot_kmeans_algorithm()

Be careful when installing the mglearn library from the Anaconda prompt.
Be sure to use the “pip install” command, not the “conda install” command.

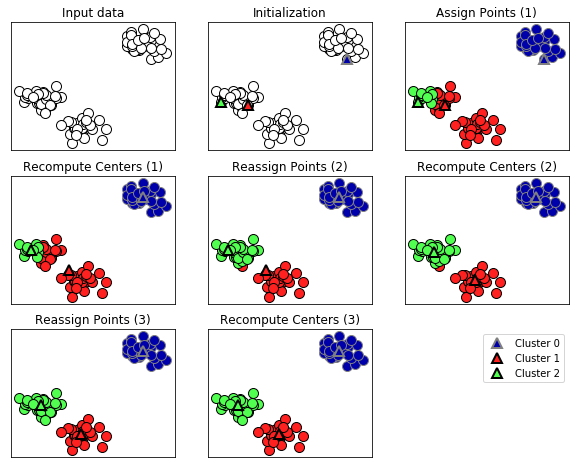
In the figure, triangles are cluster centers and circles are data points. Clusters were color coded. We specified three clusters to be found, and randomly initialized three data points to be cluster-centric. And the algorithm is repeated.
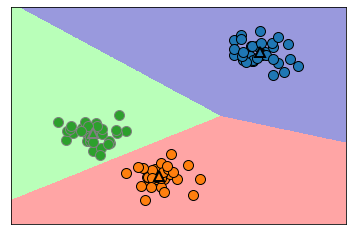
The following is the cluster center boundary learned in the above figure.

plots.plot_kmeans_boundaries()

You can also use the k-means algorithm in scikit-learn. You specify the number of clusters (in this example, 3) and then call the fit method.

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

X, y = make_blobs(random_state=1)

kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

print(kmeans.labels_)

print(kmeans.predict(X))

You can check the labels in the kmeans.labels_ property, and you’ll be numbered 0 through 2 because you’ve specified three clusters.

The predict method can be used to predict cluster labels for new data. The prediction assigns the cluster center closest to each point and does not change the existing model.

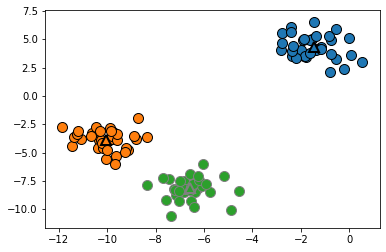
The graph of the data is as follows.

discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
discrete_scatter(
    kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
    markers='^', markeredgewidth=2)

Cases where the k-means algorithm fails

Knowing the exact number of clusters in a dataset doesn’t always succeed the k-means algorithm. Because each cluster defines only one center, the clusters appear rounded. It is difficult to apply k-means in the following cases.

When the data is different density

When data looks complicated

In this time, we learned about K-means clustering, a non-hierarchical clustering.
Next time, let’s talk about hierarchical clustering.