2020.03.14(pm): Hierarchical Clustering

We learned about K-means clustering last time. K-means clustering has a limitation that it can be used only when the density of the cluster is constant and the shape of the cluster is simplified. You also have to specify the number of clusters you want to find. Let’s take a look at the clustering algorithm that improved these disadvantages.

Agglomerative clustering

Agglomerative clustering designates each point as a cluster at the beginning, and then merges the two closest clusters until a certain termination condition is met. The termination condition used by scikit-learn is the number of clusters, and similar clusters are merged until a specified number of clusters remain. The linkage option specifies how to measure the closest cluster. This measurement is always made between two clusters.

Let’s look at the process of clustering to find three clusters in a two-dimensional dataset.

mglearn.plots.plot_agglomerative_algorithm()

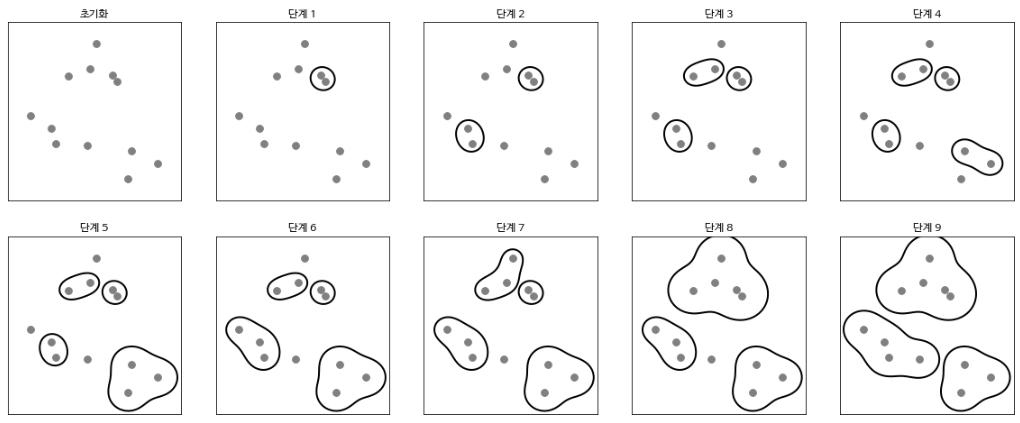
Initially, each point is a cluster. The two closest clusters at each stage are then combined. Up to the fourth stage, two clusters with only one point were selected and combined to become a cluster with two points. In step 5, one of the two-point clusters is extended to three points. When you reach Step 9 in this way, there are only three clusters left. If you specify that you want to find three clusters, the algorithm stops here.

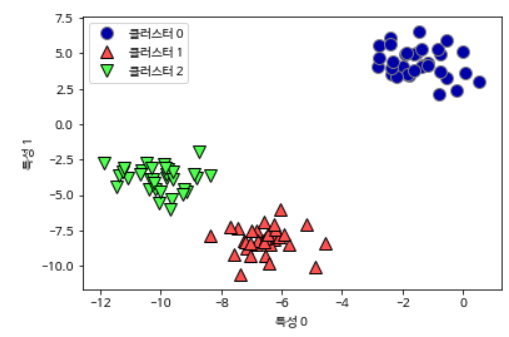
Let’s see how agglomerative clustering works with simple data with the three clusters we used earlier. Agglomerative clustering cannot predict the new data points due to the algorithm’s operational characteristics. Therefore, agglomerative clustering does not have a predict method. Instead, use the fit_predict method to build the model from the training set and get cluster membership information.

from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)

agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)

mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
plt.legend(["클러스터 0", "클러스터 1", "클러스터 2"], loc="best")
plt.xlabel("특성 0")
plt.ylabel("특성 1")

As expected, the algorithm found the cluster perfectly. To use scikit-learn’s agglomerative clustering model, you need to specify the number of clusters to find, but agglomerative clustering can also help you choose the right number.

Hierarchical clustering and Dendrogram

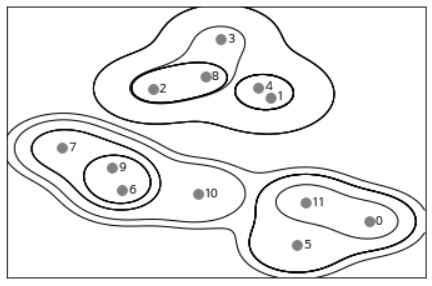
Agglomerative clustering creates hierarchical clusters. If the cluster is repeated, all points start from the cluster with one point and move to the last cluster. This helps to connect all possible clusters. The figure below shows all clusters superimposed.

mglearn.plots.plot_agglomerative()

This graph shows the details of the hierarchical cluster, but it is only for 2D data and cannot be used for datasets with more than two characteristics. So how do you deal with multidimensional data? Another tool for visualizing hierarchical clusters, dendrograms, can process multidimensional datasets.

Let’s apply Hierarchical Clustering to MNIST data set, which is numeric image data from 0 to 9.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

digits = load_digits()
n_image = 30
np.random.seed(0)
idx = np.random.choice(range(len(digits.images)), n_image)
X_image = digits.data[idx]
images = digits.images[idx]

plt.figure(figsize=(6, 3))
for i in range(n_image):
    plt.subplot(3, 10, i + 1)
    plt.imshow(images[i], cmap=plt.cm.bone)
    plt.grid(False)
    plt.xticks(())
    plt.yticks(())
    plt.title(i)

from matplotlib.offsetbox import OffsetImage, AnnotationBbox

plt.figure(figsize=(20, 8))
ax = plt.subplot()

ddata = dendrogram(Z)  

dcoord = np.array(ddata["dcoord"])
icoord = np.array(ddata["icoord"])
leaves = np.array(ddata["leaves"])
idx = np.argsort(dcoord[:, 2])
dcoord = dcoord[idx, :]
icoord = icoord[idx, :]
idx = np.argsort(Z[:, :2].ravel())
label_pos = icoord[:, 1:3].ravel()[idx][:n_image]

for i in range(n_image):
    imagebox = OffsetImage(images[i], cmap=plt.cm.bone_r, interpolation="bilinear", zoom=3)
    ab = AnnotationBbox(imagebox, (label_pos[i], 0),  box_alignment=(0.5, -0.1), 
                        bboxprops={"edgecolor" : "none"})
    ax.add_artist(ab)

plt.show()

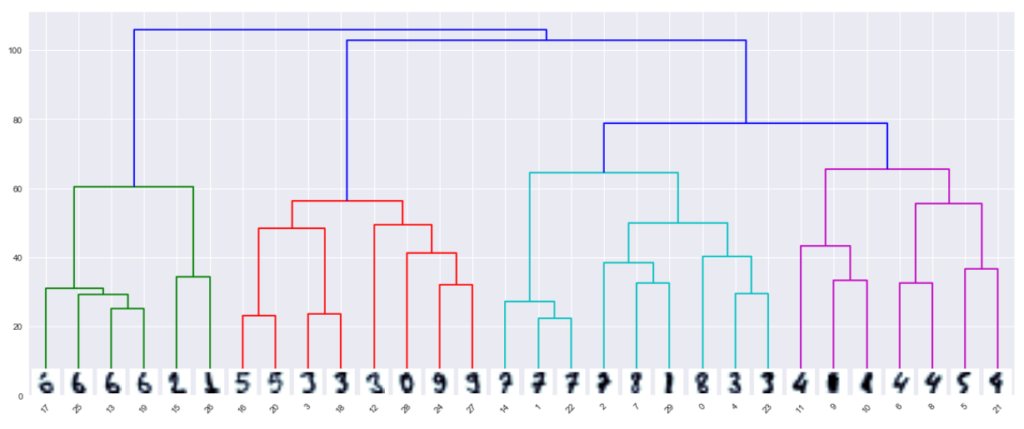
In the dendrogram, data points appear at the bottom. A tree is created with these points, each of which is a cluster, and a new parent node is added when the two clusters merge.

The y-axis of the dendrogram does not simply indicate when two clusters merge in agglomerative clustering. The length of the branches shows how far the combined clusters are.

However, agglomerative clustering does not distinguish complex shapes. But next time, let’s look at the DBSCAN algorithm that can distinguish these complex shapes.