2020.08.29(pm): Deep Learning with PYTORCH

I wrote this post with a tutorial on ending deep learning in 60 minutes via the link below.
https://tutorials.pytorch.kr/beginner/deep_learning_60min_blitz.html

What is PYTORCH?

A Python-based scientific computation package targeted at two groups:

• When computing using GPU is required while replacing NumPy
• When you need a deep learning research platform that provides maximum flexibility and speed

First, let’s install the PyTorch.

conda install pytorch torchvision cpuonly -c pytorch

Tensors

Tensor is similar to NumPy’s ndarray, and computational acceleration using GPU is also possible.

from __future__ import print_function
import torch

An uninitialized matrix has been declared, but does not contain a clearly known value until use. When an uninitialized matrix is ​​created, the values ​​existing in the allocated memory at that time are displayed as initial values.

x = torch.empty(5, 3)
print(x)

NEURAL NETWORKS

Neural networks can be created using the torch.nn package.

So far we’ve looked at autograd, nn uses autograd to define and differentiate models. nn.Module contains a forward(input) method that returns a layer and an output.

Let’s look at a neural network that classifies numeric images as an example:

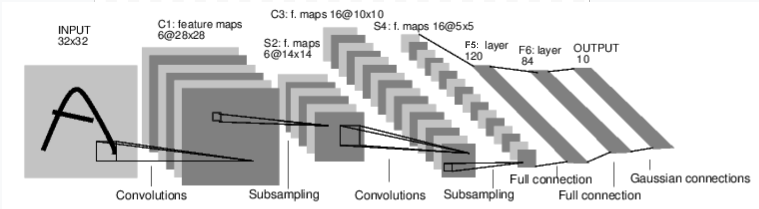
This is a simple feed-forward network. It receives input and delivers it to several layers in order, and then provides final output.

The general learning process for neural networks is as follows:

Define a neural network with learnable parameters (or weights).

Repeat the dataset input.

The input is processed in a neural network.

loss; Calculate how far the output is from the correct answer.

It propagates the gradient back to the parameters of the neural network.

Update the weights of the neural network. In general we use a simple rule like this: wiehgt = weight-learning rate * gradient

Define a neural network

Now let’s define a neural network:

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

After defining only the forward function, the backward function (which calculates the gradient) is automatically defined using autograd. You can use any Tensor operation in the forward function.

The model’s learnable parameters are returned by net.parameters().

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

Let’s put a random 32×32 input value.

Note: The expected input size of this neural network (LeNet) is 32×32. In order to use the MNIST dataset for this neural network, the image size of the dataset must be changed to 32×32.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

Set the gradient buffer to 0 for all parameters, backpropagating to a random value:

net.zero_grad()
out.backward(torch.randn(1, 10))

Loss Function

The loss function receives output and target as inputs of a pair and calculates a value that estimates how far the output is from the target.

There are several loss functions in the nn package. A simple loss function is nn.MSEloss, which computes the mean-squared error between the output and the target.

For example:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Backpropagation

To back propagate the error, you only need to do loss.backward(). It is necessary to remove the existing gradient, otherwise the gradient will accumulate on the existing one.

Now let’s call loss.backward() to look at the bias gradient of conv1 before and after backpropagation.

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

Weight update

The simplest update rule that is actually used most often is SGD; Stochastic Gradient Descent is:

wiehgt = weight-learning rate * gradient

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

When constructing a neural network, you may want to use various update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc. To do this, we have implemented all of these methods in a small package called torch.optim. It’s very simple to use:

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.01)

optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update